Multi-armed Bandit 문제 이해하기: 강화학습 탐험과 활용 방법

Multi-armed Bandit 문제 이해하기: 강화학습 탐험과 활용 방법

카지노에 가면(가본 적은 없다) 레버를 당겨 숫자를 맞추고 상금을 얻는 슬롯머신이 있다. 이를 다른 말로 Bandit이라고 하는데, 이 Bandit에 서로 다른 확률로 잭팟을 터뜨리는 레버가 있다고 가정해 보자.

 

만약 우리가 각 레버의 잭팟 확률 혹은 각 레버를 당겼을 때의 평균 보상을 알고 있다면, 우리는 가장 높은 보상 기댓값을 주는 레버만 주구장창 당기면 된다. 하지만 일반적인 상황에서 우리는 그런 정보를 사전에 알지 못한다. 그럼 어떻게 하면 보상의 기댓값을 최대화할 수 있을까?

 

이러한 문제를 Multi-armed Bandit 문제라고 한다. 이 문제에 대해서 이해해 보면서, 강화학습에서의 탐험(Exploration)과 활용(Exploitation)에 대해 알아보도록 하자.

 

Multi-armed Bandit 문제

앞서 언급했던 상황과 유사하게, Multi-armed Bandit 문제는 강화학습에서 자주 언급되는 기초적인 문제로, 여러 개의 슬롯머신이 주어졌을 때 어떤 레버를 당겨야 가장 높은 보상을 받을 수 있을지 모르는 상황을 가정한다. 여기서 'arm'은 슬롯머신에 달린 레버 (혹은, 각각의 슬롯머신)를 의미하며, 이 레버들은 서로 다른 확률 분포를 가지고 있다. 우리의 목표는 최대한 많은 보상(reward)을 얻는 것이다.

 

이 문제의 핵심은 탐험(Exploration)과 활용(Exploitation) 사이의 균형을 맞추는 데 있다. 즉, 현재까지의 경험을 바탕으로 가장 보상이 높았던 슬롯머신(활용)을 반복적으로 사용할지, 아니면 아직 충분히 탐험하지 않은 다른 슬롯머신(탐험)을 시도해 볼지 결정해야 하는 것이다.

 

각 레버를 당기는 행동(action)은 각 레버가 가지는 고유한 확률 분포에 따라 t$t$ 시점에서 보상 Rt$R_t$를 반환한다. 특정 레버 a$a$를 당겼을 때의 기대 보상은 다음과 같이 정의된다.

q∗(a)=E[Rt|At=a]

 

여기서 q∗(a)는 레버 a를 당겼을 때의 실제 기대 보상(real value)이다. 물론 이를 정확히 계산할 수 있다면 좋겠지만, 실제로는 정확한 값을 사전에 알지 못하기 때문에 우리는 이를 추정하기 위해 Qt(a)라는 값을 사용한다.

 

다시 슬롯머신으로 돌아와서, 아무런 레버도 당기지 않은 상태를 생각해 보자. 일단 우리는 가진 정보가 아무것도 없으므로, 1번부터 k번까지의 모든 레버의 초기 기댓값을 0으로 잡을 수 있다.

 

Q1(a1)=0,Q1(a2)=0,…,Q1(ak)=0

 

이제 아무 레버나 잡고 당겨보자. a2를 당겼더니, 20이라는 보상이 나왔다고 해보자. 이 경우, t=2에서의 a2의 기댓값이 업데이트된다.

 

Q2(a1)=0,Q2(a2)=20,…,Q2(ak)=0

 

이제 우리는 한 레버의 기댓값이 다른 레버의 기댓값보다 커졌다. Greedy 한 방법에서는 가장 큰 기댓값을 선택하게 되니 다시 한번 레버 a2를 당겨보도록 하자. 그랬더니 이번엔 5라는 보상이 나왔다. 이 경우 기댓값을 다음과 같이 업데이트할 수 있다.

 

Q2(a2)=20+52=12.5

 

여전히 기댓값이 0인 다른 레버들보다 높으므로, 우리는 2번 레버를 계속 당기게 될 것이다. 그런데 이게 과연 가장 좋은 선택일까?

 

당연히 아닐 확률이 매우 크다. 각 레버의 확률 분포는 사전에 설정되어 고정되어 있는 상황(Stationary)이므로, 우리는 다른 레버들도 당겨보면서 어떤 게 가장 높은 범위의 보상 확률 분포를 가지고 있는지 알아봐야 한다. 이러한 상황이 바로 '탐색(Exploration)과 활용(Exploitation)의 균형'이다.

 

과거의 이력을 바탕으로 최고의 선택을 반복하는 것을 활용, 그리고 과거 이력에서 벗어나서 랜덤 하게 선택하는 것을 탐색이라고 한다. 즉, 2번 레버를 계속 당기는 것이 활용이고, 다른 레버도 당겨보는 것이 탐색이다. 활용만 계속 진행한다면, 우리는 로컬 미니멈에 빠질 수 있다. 반면 탐색만 계속 진행한다면 그 선택은 모두 랜덤인 것이 된다. 따라서 이 둘 간의 균형을 적절히 맞추는 Non-greedy 한 방법이 필요하다.

 

입실론-그리디 방법

이처럼, 활용뿐만 아니라 탐색 또한 진행하는 방법을 입실론-그리디(epsilon-greedy) 방법이라고 한다. 입실론-그리디 방식에서는 기본적으로 활용을 이용하여 선택을 수행하지만, 어떠한 작은 확률(ϵ)에 따라 랜덤 한 선택을 수행(탐색)하게 된다. 예를 들어, 만약 2 개의 액션이 존재하고, 입실론의 값이 0.3이라면 그리디 한 선택이 선택될 확률은 다음과 같을 것이다.

 

1−ϵ+1nϵ=0.7+0.15=0.85

 

입실론 값만큼 랜덤 선택될 때, 그리디한 선택도 랜덤 선택의 대상이 된다는 점 주의하자.

 

 

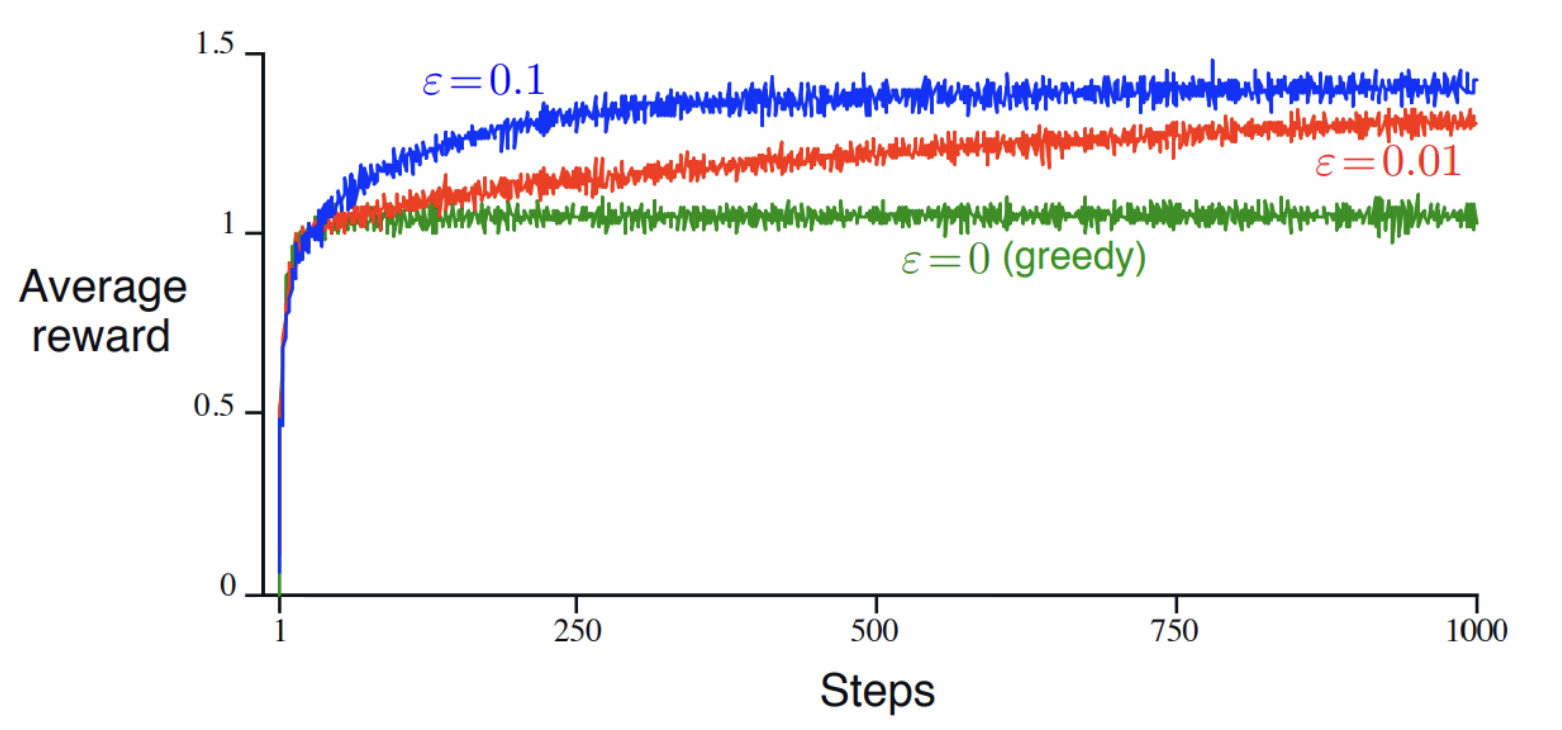
이렇게 입실론 값을 다르게 해서 여러 번 선택을 수행할 경우, 일반적으로 Greedy 한 방법(ϵ=0) 보다 입실론-그리디 한 방법의 평균 보상이 더 높은 것을 볼 수 있다.

 

Update Rule

단순히 각 스텝에서의 보상을 모두 더해서 평균 내는 산술 평균 방식은 모든 스텝에서의 리워드를 기억해야 하므로 비효율적이다. 따라서, 다음과 같은 Incremental 한 Update Rule이 주로 사용된다.

 

Qn+1=1nn∑i=1Ri=1n(Rn+n−1∑i=1Ri)

=1n(Rn+(n−1)1n−1n−1∑i=1Ri)=1n(Rn+(n−1)Qn)

=1n(Rn+n⋅Qn−Qn)=Qn+1n[Rn−Qn]

 

즉, Qn+1=Qn+1n[Rn−Qn], n+1 시점에서의 기댓값은 이전 시점 n에서의 기댓값과 실제 보상(Rn)만으로 계산이 가능하게 된다. 이렇게 되면 모든 스텝에서의 보상 값을 일일이 저장할 필요가 없어진다.

 

이처럼 간단한 Bandit 알고리즘 문제는 실제 보상값(target, Rn)과 예측된 기댓값(prediction, Qn)의 차이를 스텝 사이즈로 나눈 만큼씩 업데이트를 하는 방식으로 해결이 가능하다.

 

 

다만, 이러한 방식에는 한 가지 문제가 있다. 현재의 문제는 고정된 확률 분포(Stationary)를 가지고 있음을 가정하고 있다. 그런데 만약, 이 확률 분포가 어느 순간 갑자기 바뀐다면 어떨까? 만약 n=1,000일 때, 갑자기 확률 분포가 크게 바뀌어서 target과 prediction 사이 큰 차이가 발생했다고 해보자. 이 경우 우리는 우리의 전략을 크게 수정해야 한다. 그러나 가중치 텀이 1n이라면, 그 차이가 굉장히 작아져서 업데이트가 크게 일어나지 않을 것이다.

 

이러한 상황을 Non-stationary 한 상황이라고 하며, 이를 해결하기 위해서는 조금 다른 전략이 필요하다. 이 부분에 대해서는 다음 게시물로 다뤄보도록 하겠다.