그래프 인과모델

그래프 인과모델

구조적 인과모델(Structural Causal Model, SCM)은 인과추론의 통일된 언어 표현이다. 이 SCM은 그래프와 인과 방정식(causal equation)으로 구성된다. 그중 그래프 모델은 인과추론 문제를 구조화하고 식별 가정을 시각화할 수 있는 기법이다. 이 그래프 모델에 대해서 알아보도록 하자.

 

인과관계 시각화

처치가 무작위 배정되는 상황, 즉 처치가 잠재적 결과와 독립적이며 인과관계와 상관관계가 교환가능한 상황을 생각해 보자.

 

E[Y1−Y−0]=E[Y|T=1]−E[Y|T=0]

이러한 정보는 위 수식으로 나타낼 수도 있지만 그래프로 시각화할 수도 있다. 해당 과정에서 처치에는 랜덤화 노드를 추가하여 무작위 배정을 나타낼 수 있으며, 관측되지 않은 변수 또한 그래프에 나타낼 수 있다. 이때 관측되지 않은 변수는 모두 U 노드에 묶어서 표현한다. 여기선 그래프 시각화 라이브러리인 graphviz를 사용해서 나타내보도록 하겠다.

import graphviz as gr

g_cross_sell = gr.Digraph(graph_attr={'rankdir':'LR'})

g_cross_sell.edge('U','unwatched_var_1')
g_cross_sell.edge('U','unwatched_var_2')
g_cross_sell.edge('U','Result')

g_cross_sell.edge('Rand','Treatment')
g_cross_sell.edge('Treatment','Result')
g_cross_sell.edge('unwatched_var_1','Result')
g_cross_sell.edge('unwatched_var_2','Result')

g_cross_sell

 

그래프의 각 노드는 확률변수이다. Edge는 한 변수가 다른 변수의 원인이 됨을 나타낸다. 이러한 그래프 모델 언어는 인과관계에 대한 생각을 효과적으로 표현할 수 있도록 한다.

 

위 그림에서, unwatched_var_1과 unwatched_var_2를 하나의 노드로 묶어서 표현하는 것도 가능하며, Rand 노드를 생략하여 표현할 수도 있다.

g_cross_sell = gr.Digraph(graph_attr={'rankdir':'LR'})

g_cross_sell.edge('U','X')
g_cross_sell.edge('U','Result')

g_cross_sell.edge('Treatment','Result')
g_cross_sell.edge('X','Result')

g_cross_sell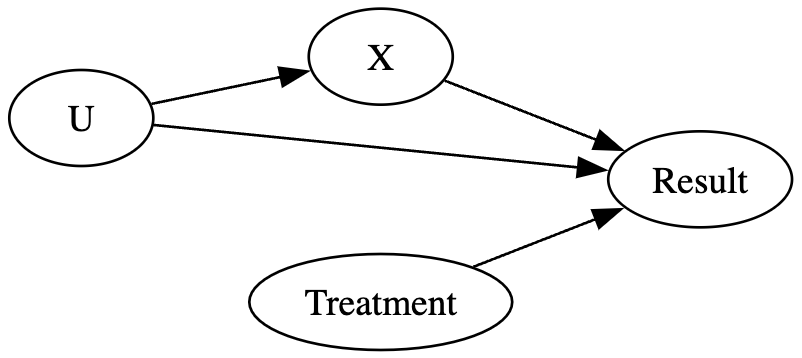

 

이처럼 그래프 인과모델은 인과관계를 시각적으로 이해할 수 있도록 하는 좋은 도구 중 하나이다. 이러한 그래프에서는 어떻게 변수를 다루는지에 따라 연관성의 흐름을 막거나 활성화할 수 있다. 이를 위한 그래프 구조 세 가지와 예시를 살펴보도록 하자.

 

그래프 구조

사슬 구조

첫 번째 구조는 가장 기본적인 그래프 구조인 사슬(chain) 구조를 알아보도록 하겠다. 처치 노드 T가 중간 노드 M의 원인이 되고, 중간 노드 M이 결과 노드 Y의 원인이 되는 상황에서, 중간 노드 M은 T와 Y 사이를 매개하는 역할을 하며 이를 매개자(mediator)라고 한다.

 

 

이 그래프 구조에서 인과관계는 화살표 방향으로만 흐르지만 연관관계는 양방향으로 흐른다. 즉, T는 M의 원인이 되고 M은 Y의 원인이 되는 단방향 흐름을 가지지만, Y는 M, 그리고 T와도 연관관계를 가진다. 이러한 경우 'T는 Y와 독립이 아니다'라고 말하며 수식적 표기로는 다음과 같이 나타낸다.

 

[Math Processing Error]

 

여기서 매개자 [Math Processing Error]을 고정하여 [Math Processing Error]의 영향을 통제하고 다른 변수들 간의 관계를 더 명확하게 이해할 수 있다. 이러한 과정을 '조건부로 설정'이라고 하며 이 경우 종속성(dependence)이 차단되어 [Math Processing Error]와 [Math Processing Error]가 독립이 된다.

 

[Math Processing Error]

 

분기 구조

두 번째 구조는 분기(fork) 구조이다. 이 구조의 특징은 하나의 원인이 두 개의 변수에 영향을 주는 공통원인(common cause)이 존재한다는 점이다.

 

 

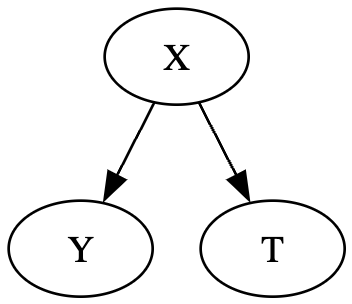
위 그림에서 [Math Processing Error]는 [Math Processing Error]와 [Math Processing Error]에 각각 영향을 주지만 [Math Processing Error]와 [Math Processing Error]는 서로 영향을 주고받지 않기 때문에(인과관계가 아니기 때문에) 둘 사이 화살표가 존재하지 않는다. 하지만 연관성이 화살표 반대 방향으로 흐르므로 둘은 함께 움직이는 상관관계를 가질 수 있다. 인과추론에서는 이처럼 처치와 결과 사이 공통원인이 존재할 때 이를 교란 변수(confounder)라고 부른다.

 

이처럼, 일반적으로 분기 구조에서 공통원인을 공유하는 두 변수 [Math Processing Error]와 [Math Processing Error]는 서로 종속이지만, 교란 변수가 고정되어 조건부로 설정되면 둘은 독립이 된다.

 

[Math Processing Error]
[Math Processing Error]

 

충돌부 구조

마지막으로 충돌부(collider) 구조를 살펴보도록 하자. 충돌부 구조는 두 노드가 하나의 자식(child)을 공유하지만 둘 사이 직접적인 관계가 없는 구조로, 두 변수가 공통의 효과를 공유하는 경우이다. 이 두 개의 화살표가 충돌하는 부분을 충돌부라고 한다.

 

 

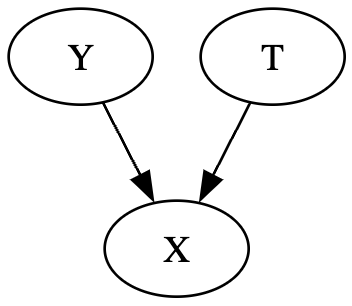
일반적으로 충돌부 구조에서 두 부모는 서로 독립이지만 공통 효과를 조건부로 두면 연관 경로가 열리면서 종속이 된다. 이는 한 가지 원인이 이미 효과를 설명하므로 다른 원인의 가능성이 더 낮아지기 때문이다. 이를 다른 요인에 의해 설명되는(explaining away) 현상이라고 한다.

 

[Math Processing Error]
[Math Processing Error]

 

여기서 재밌는 점은, 충돌부에 대한 조건부 대신, 충돌부의 효과에 조건부를 두어도 동일한 종속 경로(dependence path)를 열 수 있고 두 충돌부 원인을 서로 종속으로 만들 수 있다는 점이다.

 

 

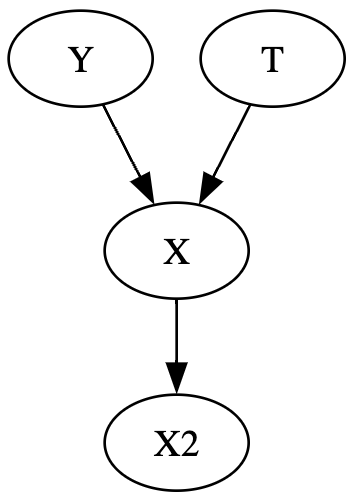
종속성 흐름

이처럼 인과 그래프모델에는 다양한 구조가 존재하며, 각 구조별, 조건부별로 종속성이 흐르는지를 기억하는 것은 중요하다. 기본적으로는 다음과 같은 필요충분조건에 따라 차단될 수 있다

1. 조건으로 주어진 비충돌부 구조가 포함
2. 조건부로 주어지지 않고 자식이 없는 충돌부가 포함

이러한 규칙을 잘 이해하고 적용해 보는 연습이 중요하다. 그리고, 다음 게시글에서는 이러한 종속성을 파이썬으로 쿼리 하는 방법에 대해서 알아보도록 하자.